index

Introduction

This CTF I played with Cosmic Bit Flip. We managed to get a calm 1st place high school win! Thanks to all of my orz teammates:

c-bass
anywheres
wjat
brew
mathlegend

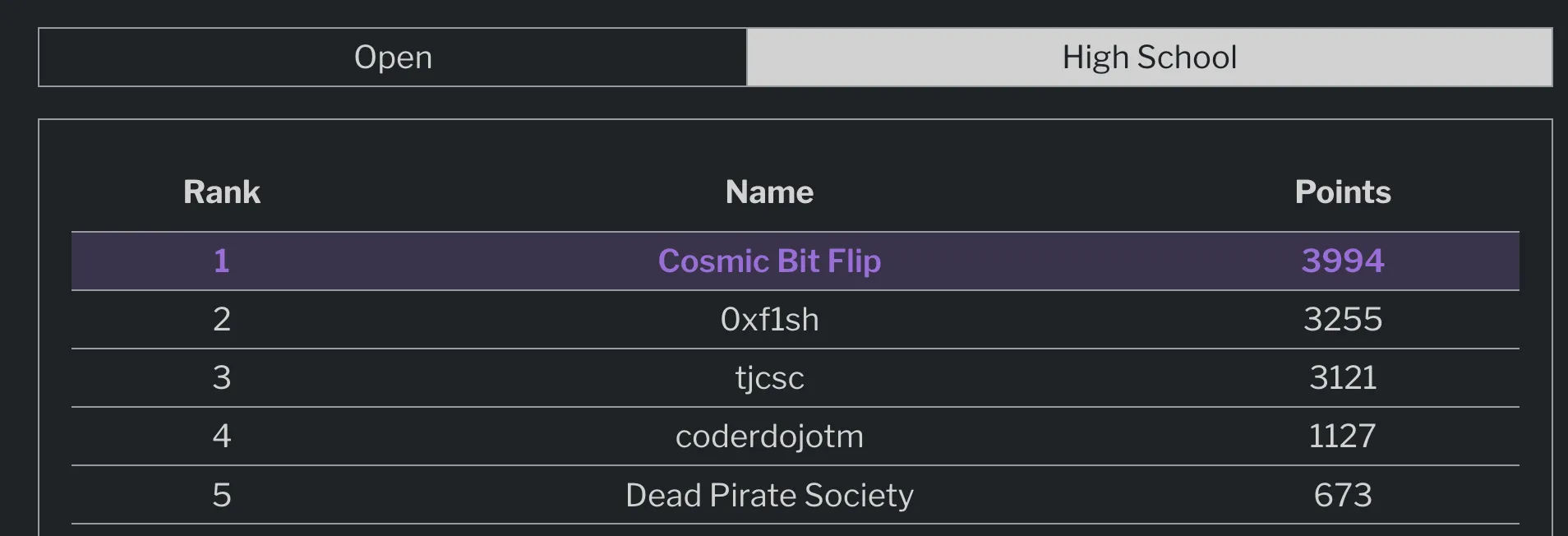
leaderboard

More thanks to les amateurs for organizing a great CTF with high quality challenges.

Here I’ll write about two crypto challenges that wjat and I solved using a timing side-channel.

add3

What the server did

1
from Crypto.Util.number import *
2
from random import getrandbits, choice
3
import hashlib
4

5
flag = open('flag.txt','rb').read().strip()
6
assert len(flag) == 72
7
flag = bytes_to_long(flag) << 256
8

9
n = getPrime(1024) * getPrime(1024)
10
e = 3
11

12
print(f'{n, e = }')
13

14
while True:
15
    cs = [flag + getrandbits(256) for _ in range(100000)]
16
    scramble = int(input('scramble the flag: '))
17

18
    ms = [(m + scramble)%n for m in cs]
19

20
    print('scrambling...')
21

22
    c = choice([pow(m, e, n) for m in ms])
23
    print(f'{c = }')

That was the server for the first challenge, addition2. The second one (addition3) only had a few minor changes:

1
from Crypto.Util.number import *
2
import os
3
from random import getrandbits, choice
4
import hashlib
5

6
flag = open('flag.txt','rb').read().strip()
7
assert len(flag) == 52
8

9
flag = bytes_to_long(flag) << 512
10

11
while True:
12

13
    n = int(os.popen('openssl genrsa 2048 | openssl rsa -noout -modulus').read()[8:], 16)
14
    e = 3
15

16
    print(f'{n, e = }')
17
    cs = [flag + getrandbits(512) for _ in range(100000)]
18
    scramble = int(input('scramble the flag: '))
19

20
    ms = [(m + scramble)%n for m in cs]
21

22
    print('scrambling...')
23

24
    c = choice([pow(m, e, n) for m in ms])
25
    print(f'{c = }')%

Here, the server:

Generates an RSA modulus $n$ and uses $e = 3$ , then prints these values
It builds a list cs = [flag_shifted + getrandbits(K) for _ in range(100000)].

addition2: flag shifted left 256 bits, $K = 256$ .
addition3: flag shifted left 512 bits, $K = 512$ .

It asks for an integer $\text{scramble}$ .
It computes ms = [(m + scramble) % n for m in cs].
It computes cands = [pow(m, e, n) for m in cs], and prints one random choice of these ciphertexts.

Key observation: the inner loops are repeated 100,000 times, implying that tiny timing differences are massively amplified.

Where’s the leak?

Let $F$ be the integer flag after the left shift ( $F = \text{flag} << \text{shift}$ ). For a candidate padding $r$ we have $m = F + r$ , $r$ being the random bytes. When we send a scramble $S$ the server computes:

A = m + S = F + r + S

Now, two operations within the 100k loop depend on $A$ :

Reduction: A % n
Modular exponentiation: pow(A, e, n). This computes $A^e \pmod{n}$ . The cost of this grows with the bit-length of the base $A$ . If $A$ is small, then repeated exponentiation is faster; if $A$ is near $n$ when mod $n$ , exponentiation is much slower.

We found in practice that pow dominates the wall-clock difference on our machine: large effecive bases lead to much slower pow, amplified by 100k. Roughly, it might take $3$ seconds instead of $0.5$ .

A very robust probe is to send $S = -F_{\text{guess}}$ .

Then per candidate:

A = (F + r) - F_\text{guess} = (F - F_\text{guess}) + r

If $F_\text{guess} << F$ , $(F - F_\text{guess})$ is large positive and dominates $r$ , leading to a positive $A$ and a small base, making it FAST.
If $F_\text{guess} > F$ , $(F - F_\text{guess})$ is negative and dominates $r$ , leading to a negative $A$ and a large base, making it SLOW.

Note that a positive $A = (F + r + S)$ is going to be much smaller than $n$ . So, when it is positive, $A \pmod{n} \equiv A$ , which is a small base for pow. When $A$ is negative, $A \pmod{n}$ becomes $n - |A|$ (a number very close to $n$ ), which is a huge base.

This gives us a stable oracle to search for the flag: FAST $\implies$ guess too low, SLOW $\implies$ guess too high.

How we turned the timing leak into an attack

For addition2, we could do a whole-value binary search ont he value $F$ . This only look roughly 500 or so queries, and if we used the flag format this would reduce further.

For addition3, there was more noise introduced (512 bits), so we did a byte-by-byte guess, and used null byte padding as a suffix. This makes guesses monotonically ordered by the byte we are testing; the transition FAST to SLOW falls exactly at the correct byte.

Solve script for addition2

1
import time
2
from tqdm import trange
3
from pwn import *
4
from Crypto.Util.number import *
5

6
g1 = b"amateursCTF{" + bytes(48) + b"}"
7
g1 = bytes_to_long(g1) << 256
8
g2 = b"amateursCTF{" + bytes(48) + b"}"
9
g2 = bytes_to_long(g2) << 256
10

11
def get_time(sus_flag):
12
    chall.sendline(str(-sus_flag).encode())
13
    start = time.time()
14
    chall.recvuntil(b':')
15
    return time.time() - start
16

17
chall = process(['python3', 'chall.py'])
18
# chall = remote('amt.rs', 38593)
19
msg = chall.recvuntil(b':').decode()
20

21
for _ in trange(472):
22
    g3 = (g1 + g2)//2
23
    if get_time(g3) >= 1:
24
        g2 = g3
25
    else:
26
        g1 = g3
27

28
print(long_to_bytes(g3))

That’s the binary-search approach, here is the solve script for addition3:

Solve script for addition3

1
#!/usr/bin/env python3
2
from pwn import *
3
from Crypto.Util.number import *
4
import time
5

6
LOCAL = False
7
TIME_THRESHOLD = 1.5
8

9
FLAG_LEN = 52
10
FLAG_SHIFT = 512
11
RANDOM_BITS = 512
12

13
PREFIX = b"amateursCTF{"
14
SUFFIX = b""
15
MIDDLE_LEN = FLAG_LEN - len(PREFIX) - len(SUFFIX)
16

17
CHARSET = list(range(48, 127))
18

19
def get_connection():
20
    if LOCAL:
21
        return process(['python3', 'chall.py'])
22
    else:
23
        return remote('amt.rs', 5959)
24

25
def solve():
26
    known_middle = b""
27
    r_max = (2**RANDOM_BITS) - 1
28

29
    conn = get_connection()
30

31
    n_line = conn.recvline().decode()
32
    n, e = eval(n_line.split(" = ")[1])
33

34
    for i in range(MIDDLE_LEN):
35
        log.info(f"Solving for byte {i}...")
36
        last_fast_byte = -1
37

38
        for b_val in CHARSET:
39
            current_middle_guess = known_middle + bytes([b_val])
40
            padded_middle = current_middle_guess.ljust(MIDDLE_LEN, b'\x00')
41
            full_guess_bytes = PREFIX + padded_middle + SUFFIX
42

43
            F_guess = bytes_to_long(full_guess_bytes) << FLAG_SHIFT
44

45
            scramble = n - r_max - F_guess
46
            conn.recvuntil(b'scramble the flag: ')
47

48
            start_time = time.time()
49
            conn.sendline(str(scramble).encode())
50

51
            conn.recvline()
52
            conn.recvline()
53
            duration = time.time() - start_time
54
            print(f"duration was {duration} for char {b_val}")
55

56
            n_line = conn.recvline().decode()
57
            n, e = eval(n_line.split(" = ")[1])
58

59
            if duration < TIME_THRESHOLD:
60
                last_fast_byte = b_val
61
            else:
62
                log.info(f"  -> Guess '{chr(b_val)}' was SLOW ({duration:.2f}s). Transition found.")
63
                break
64

65
        if last_fast_byte == -1:
66
            log.error(f"Failed to find any fast response for byte {i}. Threshold might be wrong or char not in charset.")
67
            break
68

69
        known_middle += bytes([last_fast_byte])
70
        log.success(f"Solved byte {i}: {PREFIX.decode()}{known_middle.decode()}...")
71

72
    final_flag = PREFIX + known_middle + SUFFIX
73
    log.success(f"Recovered Flag: {final_flag.decode()}")
74
    conn.close()
75

76
if __name__ == "__main__":
77
    solve()

This is the byte-by-byte approach. It takes a bit longer, but progress persists across instances, so that’s okay. Also, the charset within the flag format turned out to be lowercase hex, so that could have been optimized.

Conclusion

Wjat and I were stuck on this for a long time. We tried and failed to implement multivariate coppersmith for addition2 and were completely stumped for addition3. Eventually though, we thought of this timing side channel and managed to solve both.

I guess the lesson is that in creating cryptographically secure services, you always need to watch out for any side-channel that can leak information about secrets! By manipulating our controlled value (scramble) to probe for timing differences, we managed to leak the entire flag, even though the cryptosystem itself is secure.

amateursCTF 2025